Dynamic Programming

Dynamic Programming 是一種在計算機科學和數學中常用的問題解決方法。

它的主要策略是將一個複雜的問題拆解成較小的子問題，然後將這些子問題的解保存起來，以避免重複計算，從而提高效率。動態規劃通常適用於具有重疊子問題結構和最優子結構性質的問題。

動態規劃的步驟包括：

1. 定義問題：明確地定義原始問題和子問題。
2. 建立狀態轉移方程：找到子問題之間的關係，通常以遞迴方式表示。
3. 初始化：初始化一個數組或表格，用於保存子問題的解。
4. 自底向上求解：從最小的子問題開始，根據狀態轉移方程計算並保存解，逐步解決較大的問題，直到解決原始問題。

動態規劃可以應用於各種不同的問題，包括最優化、排程、路徑搜索和序列比對等。

Fibonacci Sequence

首先來個簡單的

Fibonacci Sequence 是一個數學數列，其中每一個數字都是前兩個數字的和。

它通常以F(n)表示，其中n是數列的索引，從0開始。

這個數列的前幾個數字是0、1、1、2、3、5、8、13、21，以此類推。

費波那契數列的數學定義如下：

// Fibonacci Sequence
class Fibonacci {
    fun fib(n: Int): Int {
        if (n <= 1) return n
        return fib(n - 1) + fib(n - 2)
    }
}

// main function
fun main(args: Array<String>) {
    val fib = Fibonacci()
    println("Fibonacci(5) = ${fib.fib(5)}")
    println("Fibonacci(10) = ${fib.fib(10)}")
    println("Fibonacci(20) = ${fib.fib(20)}")
}

Longest Common Subsequence

Longest Common Subsequence (LCS) 用來表示兩個序列中最長的共同子序列。

演算法

1. 首先，建立一個二維矩陣（通常稱為LCS矩陣），其維度為，其中和分別為兩個輸入字串的長度。
2. 初始化LCS矩陣的第一列和第一行為零，這表示空字串與任何字串的LCS長度都為零。
3. 依次比較兩個字串的每個字符。如果字符相等，則將LCS矩陣中當前位置的值設為左上角對角線上的值加一，表示LCS長度增加一。
4. 如果字符不相等，則將LCS矩陣中當前位置的值設為左方和上方兩個相鄰位置中的較大值，表示要銜接LCS。
5. 繼續填充LCS矩陣，直到達到右下角，這將包含兩個輸入字串的最長公共子序列的長度。
6. 最後，根據填充後的LCS矩陣，可以反向遍歷矩陣，從右下角開始，來重建最長公共子序列。

// Longest Common Subsequence in Kotlin

class LCS {
    fun lcs(X: String, Y: String, m: Int, n: Int): Int {
        val L = Array(m + 1) { IntArray(n + 1) }
        for (i in 0..m) {
            for (j in 0..n) {
                if (i == 0 || j == 0) {
                    L[i][j] = 0
                } else if (X[i - 1] == Y[j - 1]) {
                    L[i][j] = L[i - 1][j - 1] + 1
                } else {
                    L[i][j] = Math.max(L[i - 1][j], L[i][j - 1])
                }
            }
        }
        return L[m][n]
    }
}

// main function
fun main(args: Array<String>) {
    val X = "AGGTAB"
    val Y = "GXTXAYB"
    val m = X.length
    val n = Y.length
    val lcs = LCS()
    println("Length of LCS is ${lcs.lcs(X, Y, m, n)}")
}

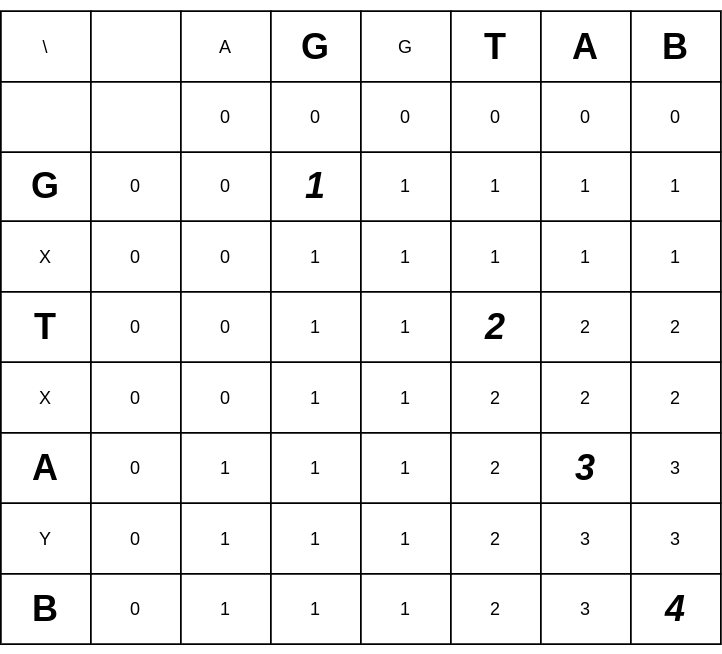
透過上述結果，我們可以找到 Longest Common Subsequence (LCS) 結果是 GTAB

所有 Code 可以在 Github 找到 ～

接下來明天要講解

• Longest Increasing Subsequence
• 0-1 Knapsack Problem